Дорогой друг!
Приглашаем тебя принять участие в заочном конкурсе пo математике. Участвовать в нём может любой ученик 6-8 класса, решивший по крайней мере пять из предлагаемых 20 задач. Для этого он должен не позднее 27 октября выслать полные решения задач (не только ответы!) обычным письмом (не заказным) по адресу
Москва, 119002, Большой Власьевский пер., дом 11, Московский центр непрерывного математического образования, заочный конкурс, ... класс.
На письме должен быть указан обратный адрес, включая имя и фамилию. В письмо следует вложить два пустых незаклеенных конверта с маркой, написав на них свой адрес (В одном конверте будут посланы результаты проверки и приглашение на разбор. Другой конверт может быть использован для информации о заочном конкурсе, математических кружках, олимпиадах и пр.)
На каждом листе работы просим указывать фамилию, имя, номер школы и класс. В письмо следует вложить заполненную карточку участника.
Справки по всем вопросам, связанным с конкурсом, можно получить по телефону (495) 945-82-16 (попросить соединить с организаторами заочного конкурса), а также по электронной почте: zmk@mccme.ru. (Очень просим Вас НЕ присылать решения по электронной почте.)
На сайте http://www.mccme.ru/ имеется также информация о математических кружках, олимпиадах и пр. Информацию о кружках можно получить также по телефону (499) 241-05-00.
Желаем успеха!
1. Какова может быть суммарная длительность подряд идущих 11 месяцев, выраженная в днях (сутках)? Укажите все возможности.
2. Два поезда разной длины едут навстречу друг другу с разными (но постоянными для каждого поезда) скоростями. В одном из поездов ехали (в разных вагонах) Миша и Коля, в другом Маша и Лена. Миша повстречался с Машей ровно в полдень (они проехали друг мимо друга), а с Леной в 12:02. Когда Коля повстречался с Машей, если с Леной они встретились в 12:05?
3. Можно ли спаять из кусков проволоки фигуру, которая спереди выглядит как M, а слева как Z (см. рисунок)? Если можно, как она будет выглядеть сверху?


4. Найдите наибольшее целое положительное число, в котором все цифры разные, а любые две подряд идущие цифры образуют двузначное число, делящееся на 7.
5. Двух игроков команды помещают в разные комнаты и дают им по карточке белого или чёрного цвета. Каждому игроку предлагают назвать цвет карточки, которую дали его партнёру. Команда выигрывает, если хотя бы одному игроку удалось сделать это правильно. Могут ли они договориться заранее о действиях в такой ситуации, которые бы гарантировали выигрыш?
6. Если из левой кучи переложить одно яблоко в правую, то яблок в обеих будет одинаковое число. А если наоборот, из правой в левую, то в левой будет в два раза больше. Сколько яблок в каждой куче?
7. Прямоугольный равнобедренный треугольник, сделанный из фанеры, лежит на плоскости. Его можно перекатывать по плоскости вокруг любой из сторон (симметрично отражая относительно неё). Может ли он после нескольких перекатываний оказаться в положении, показанном пунктиром?
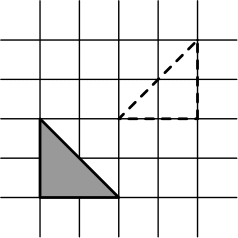
8. Можно ли после нескольких перекатываний вернуть треугольник в исходное положение, но перевёрнутым другой стороной?
9. Муравьи на кольцевой дорожке длиной 60 см движутся в обе стороны с постоянной скоростью 1 см в секунду. Когда два муравья сталкиваются, они оба разворачиваются, двигаясь в противоположном направлении с той же скоростью (считаем, что мгновенно, и пренебрегаем размером муравьёв, считая их точками). Оказалось, что каждую минуту происходят 48 таких столкновений. Сколько муравьёв на дорожке? Укажите все возможные варианты.
10. Внутри квадрата взята точка. Известно, что её расстояния до трёх сторон квадрата равны (в каком-то порядке) 1, 3, 6. Каким может быть расстояние до четвёртой стороны? Укажите все варианты.
11. По кругу в произвольном порядке расставлены цифры 0, 1, 2, 3, …, 9, каждая по одному разу. Для каждой пары соседних цифр подсчитали их разницу (положительное число), и все эти числа сложили. Какой наибольший результат мог получиться? Приведите пример такой расстановки и покажите, что больше быть не может.
12. (Продолжение) Сколькими способами этот наибольший результат можно получить? (Способы, отличающиеся лишь поворотом окружности, не различаются.)
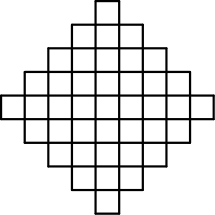
13. Наклонный квадрат на клетчатой бумаге (см. рисунок) хотят замостить доминошками 1×2 (без пробелов и перекрытий). Докажите, что это не удастся. Какое максимальное число доминошек можно поместить внутрь этой фигуры без пересечений?
14. Вернувшись из похода, шесть его участников подсчитали, сколько они потратили на поход. Выяснилось, что один из них потратил больше среднего на 17 рублей, другой меньше среднего на 23, третий — больше на 13 рублей, четвёртый — меньше на 29, пятый — больше на 10, шестой — больше на 12 рублей. Они хотят рассчитаться (скомпенсировать разницу) почтовыми переводами. Какое минимальное количество переводов (в каждом отправитель посылает какую-то сумму денег адресату) им потребуется?
15. Купец купил 138 аршин черного и синего сукна за 540 руб. Спрашивается, сколько аршин купил он того и другого, если синее стоило 5 руб. за аршин, а черное 3 руб.? (Из рассказа Чехова «Репетитор».)
16. На какое наименьшее целое положительное число нужно умножить бесконечную десятичную дробь 0,242424… (24 в периоде), чтобы получилось целое число?
17. Известно, что числа 2x+3y и 3x+7y оба целые. Следует ли отсюда, что числа x и y целые, или они могут быть и дробными?
18. Тот же вопрос, если известно, что числа 2x+3y и 3x+4y целые.
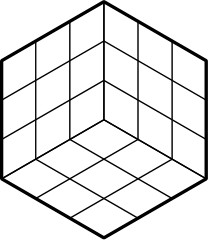
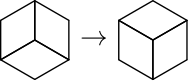
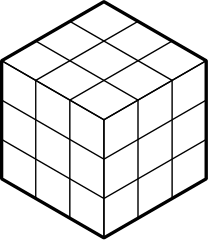
19. Шестиугольная площадка замощена ромбическими плитками (с углами 60 и 120 градусов), как показано на левом рисунке. За один день рабочие могут разобрать и переуложить три плитки внутри маленького шестиугольника (средний рисунок) . Сколько дней понадобится, чтобы переложить плитки как на правом рисунке? Объясните, почему ваш способ оптимален (за меньшее число дней не получится).
20. Что больше: 101100 или 2×10200?