
Валентина Алексеевна Кириченко
Танглы Конвея и модулярная группа
В. А. Кириченко планирует провести 4 занятия.
Доступны 4 видеозаписи курса.
Доступны материалы к курсу.
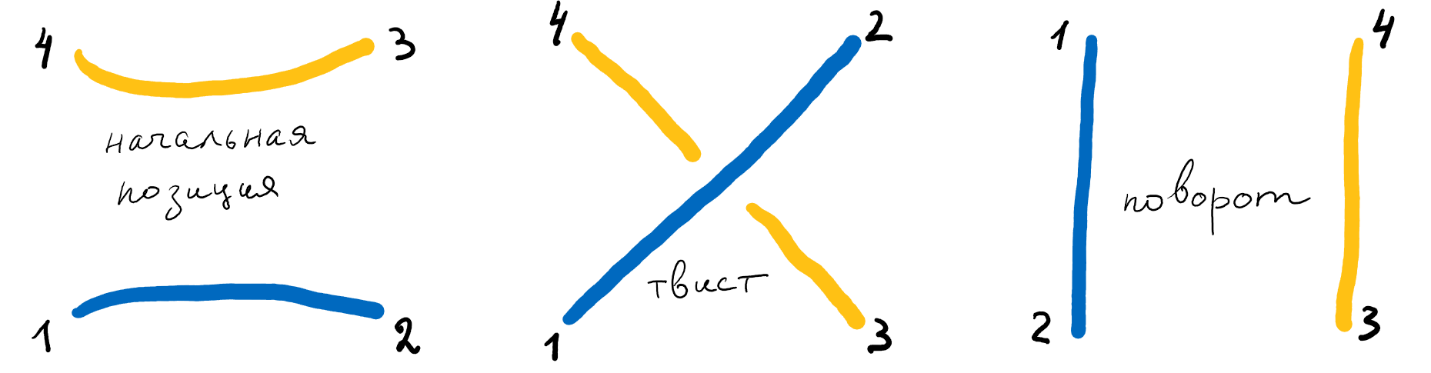
Рациональные танглы Конвея — это переплетения двух канатов, которые 4 человека с двумя канатами могут станцевать из «начальной позиции» с помощью движений «твист» и «поворот»:
По каждому танглу можно определить рациональное число — инвариант тангла относительно естественного отношения эквивалентности (два тангла эквивалентны, если один можно получить из другого, двигая канаты, но не меняя положения их концов). У твистов и поворотов есть и другие инкарнации — можно определить их действие на полуокружностях диаграммы Фарея и на параллелограммах с вершинами в узлах клетчатой бумаги. Всё это примеры действия модулярной группы. В курсе планируется подробно разобрать все приведённые выше примеры, изучить их взаимосвязи и попутно познакомиться с важными математическими объектами, такими как модулярная группа.
Программа курса:
- Как станцевать тангл Конвея и построить его полный инвариант. Узлы, танглы и зацепления: зачем Конвей придумал танглы.
- Диаграмма и дроби Фарея. Комплексная плоскость и её дробно-линейные преобразования. Связь диаграммы Фарея с разложением рационального числа в цепную дробь.
- Параллелограммы на клетчатой бумаге. Линейные отображения плоскости и преобразования решётки. Модулярная группа.
- Как склеить тор из плоскости с решёткой. Связь между параллелограммами и танглами: естественная конструкция инвариантов танглов.
Пререквизиты: курс ориентирован на школьников, и не предполагает никаких знаний, выходящих за рамки стандартной школьной программы.
Программа курсов и семинаров МЦНМО-НМУ в весеннем семестре 2024/2025 года
Расписание занятий в этом семестре
Курсы, читавшиеся в НМУ в разные годы (All Courses)
Если не указано иное, то начало занятий 7 февраля 2025.
Все обязательные курсы, почти все спецкурсы и некоторые доклады на спецсеминарах будут записываться на видео. Они будут доступны на общедоступном ресурсе.
К ВИДЕО-записям курсов этого семестра
Обязательные курсы
Первый курс
- Константин Валерьевич Логинов
- Алгебра-2
- читается по понедельникам с 17:30, очно+трансляция.
- Георгий Черных
- Топология-1
- читается по четвергам с 17:30, очно+трансляция.
- Олег Карлович Шейнман
- Математический анализ-2
- читается по пятницам с 17:30, очно+трансляция.
Второй курс
- Тарас Евгеньевич Панов
- Топология-3
- читается по понедельникам с 17:30 (семинары с 19:20), очно+трансляция
- Алексей Викторович Пенской
- Дифференциальная геометрия
- читается по средам с 17:30 (семинары с 19:20), очно+трансляция
- Алексей Игоревич Ильин
- Алгебра-4 (Группы и алгебры Ли)
- читается по четвергам с 17:30, очно+трансляция.
Список спецкурсов и спецсеминаров в весеннем семестре 2024/2025 года
- Михаил Юрьевич Розенблюм
- Алгебраическая теория чисел: введения. Продолжение годового спецкурса
- Денис Николаевич Терешкин
- Аддитивные и абелевы категории. Спецкурс рекомендован для 3-5 курсов.
- Константин Валерьевич Логинов
- Введение в ограниченность многообразий Фано. Спецкурс рекомендован для 3-5 курсов.
- Георгий Игоревич Шарыгин
- Циклические гомологии и их применения. Спецкурс рекомендован для 3-5 курсов.
- Андроник Арамович Арутюнов
- Грубая геометрия. Спецкурс в формате лекция + семинар, рекомендован для 3-5 курсов.
- Андрей Дмитриевич Рябичев
- Введение в поверхности бесконечного типа. Спецкурс рекомендован для 3-5 курсов.
- Георгий Борисович Шабат
- Тэта-функции и решетки. Часть 2. Спецкурс рекомендован для 3-5 курсов.
- Тарас Евгеньевич Панов
- Торическая топология, комбинаторика и теория гомотопий. Спецсеминар
- Георгий Игоревич Шарыгин и др.
- Деформационное квантование и квантовые группы. Спецсеминар
- А.М.Вербовецкий и И.С.Красильщик
- Когомологические аспекты геометрии дифференциальных уравнений,
руководители А.М.Вербовецкий и И.С.Красильщик - Николай Германович Мощевитин
- Диофантовы приближения. Спецсеминар рекомендован для 3-5 курсов
- Владимир Олегович Медведев
- Геометрия общей теории относительности. Спецкурс совместно с матфаком ВШЭ, рекомендован для 3-5 курсов.
- Алексей Викторович Пенской
- Риманова геометрия. Спецкурс совместно с матфаком ВШЭ, рекомендован для 3-5 курсов.
- Александр Борисович Калмынин
- Методы решета. Спецкурс рекомендован для 3-5 курсов.
- Алексей Викторович Пенской
- Спектральная геометрия. Спецсеминар рекомендован для 3-5 курсов.
