
Валентина Алексеевна Кириченко
Танглы Конвея и модулярная группа
В. А. Кириченко планирует провести 4 занятия.
Доступны 4 видеозаписи курса.
Доступны материалы к курсу.
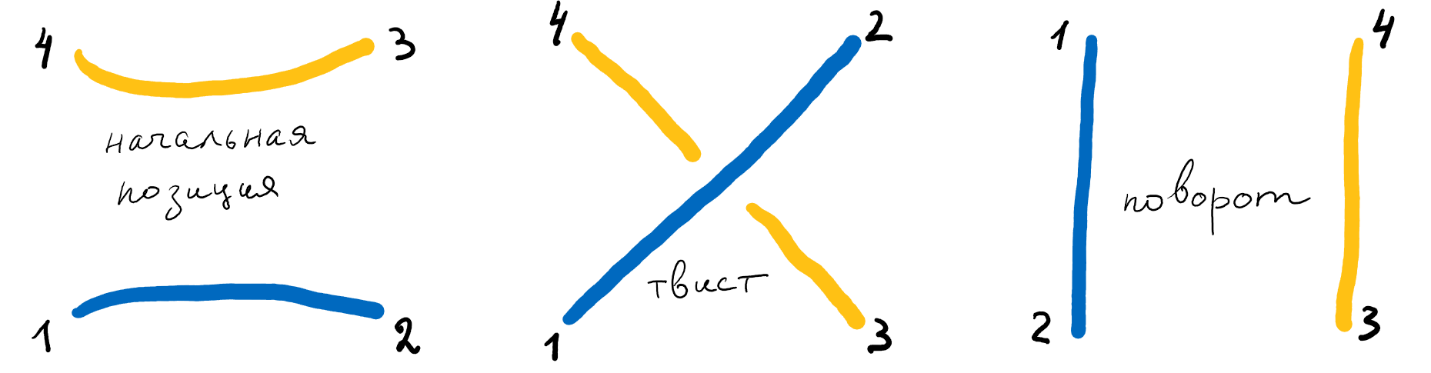
Рациональные танглы Конвея — это переплетения двух канатов, которые 4 человека с двумя канатами могут станцевать из «начальной позиции» с помощью движений «твист» и «поворот»:
По каждому танглу можно определить рациональное число — инвариант тангла относительно естественного отношения эквивалентности (два тангла эквивалентны, если один можно получить из другого, двигая канаты, но не меняя положения их концов). У твистов и поворотов есть и другие инкарнации — можно определить их действие на полуокружностях диаграммы Фарея и на параллелограммах с вершинами в узлах клетчатой бумаги. Всё это примеры действия модулярной группы. В курсе планируется подробно разобрать все приведённые выше примеры, изучить их взаимосвязи и попутно познакомиться с важными математическими объектами, такими как модулярная группа.
Программа курса:
- Как станцевать тангл Конвея и построить его полный инвариант. Узлы, танглы и зацепления: зачем Конвей придумал танглы.
- Диаграмма и дроби Фарея. Комплексная плоскость и её дробно-линейные преобразования. Связь диаграммы Фарея с разложением рационального числа в цепную дробь.
- Параллелограммы на клетчатой бумаге. Линейные отображения плоскости и преобразования решётки. Модулярная группа.
- Как склеить тор из плоскости с решёткой. Связь между параллелограммами и танглами: естественная конструкция инвариантов танглов.
Пререквизиты: курс ориентирован на школьников, и не предполагает никаких знаний, выходящих за рамки стандартной школьной программы.
Organization Committee e-mail:
dubna@mccme.ru
