

Алексей Яковлевич Канель-Белов и Филипп Дмитриевич Рухович
Внешние бильярды
А. Я. Канель-Белов и Ф. Д. Рухович планируют провести 3-4 занятия.
Доступны 4 видеозаписи курса.
Рассмотрим многоугольник Γ. Из точки p на плоскости проведем касательную (т.е. опорную прямую) к M и отразим p относительно точки касания. Такое преобразование называется преобразованием внешнего биллиарда. При последовательном применении такой операции точка может оказаться периодической (т.е. вернуться в какой-то момент в себя), апериодической (никогда не вернуться в себя), а также вырожденной (внешний биллиард можно применить конечное число раз).
Особое место занимает случай, когда Γ есть правильный n-угольник. В случаях n=3,4,6 (ϕ(n)=2) ситуация проста (апериодических траекторий нет); также ситуация была исследована для случая n=5 и, частично, n=10 (апериодическая точка есть, но периодические точки образуют множество полной меры). Автором были получены результаты для случаев n=8,12,10. Таким образом, были полностью исследованы случаи n с ϕ(n)=4. При этом, при исследовании 12-угольника были использованы доказательные компьютерные вычисления.
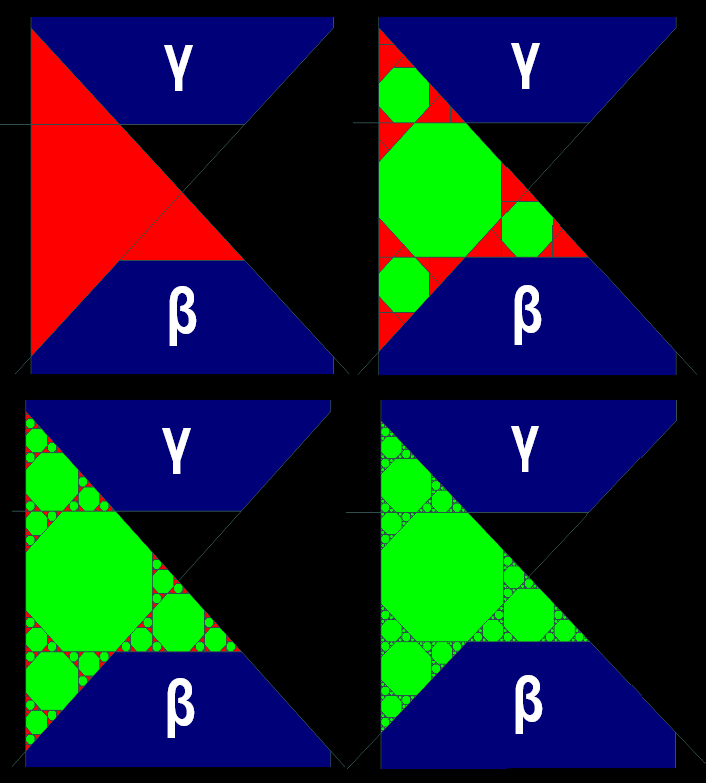
Мы расскажем как устроены периодические, апериодические и вырожденные точки, какие интересные фрактальные структуры возникают, как описать все возможные периодические компоненты, какие факты удается доказать в общем случае, а какие — только в частных случаях, какие алгоритмы могут быть полезны для обнаружения и доказательства самоподобия, и почему компьютер оказывается практически необходимым для полноценного исследования. Будут показаны некоторые занятные картинки.
Organization Committee e-mail:
dubna@mccme.ru
