Владлен Анатольевич Тиморин

Скрученные кролики

В. А. Тиморин планирует провести 2 занятия.

Доступны 2 видеозаписи курса.

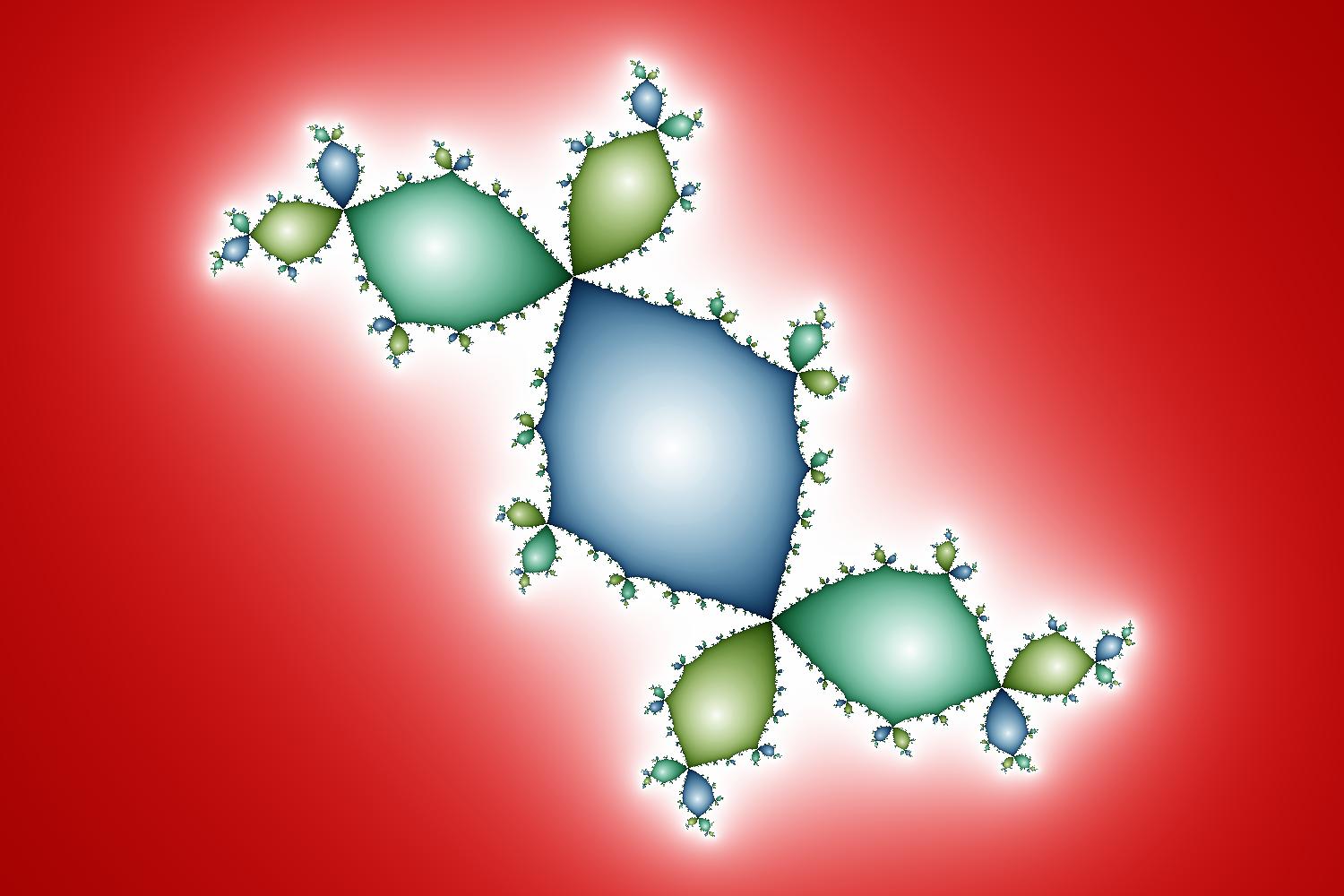
Скручивать уши у настоящих кроликов, разумеется, никто не будет. Под кроликом имеется в виду «кролик Дуади» — фрактальная фигура, возникающая как множество точек z на плоскости комплексных чисел, орбиты которых под действием квадратного многочлена p(z)=z²+c не убегают на бесконечность. Здесь c — комплексный корень кубического уравнения c³+2c²+c+1=0 с положительной мнимой частью.

Многочлен p называется отображением кролика. Два других корня того же кубического уравнения дают два других многочлена, называемых отображением антикролика и отображением самолета. Смысл названий я постараюсь объяснить.

Отображения кролика, антикролика и самолета представляют собой интересные примеры динамических систем. На примере этих отображений интересно проиллюстрировать замечательную теорию В. Терстона, которая позволяет рассматривать такие алгебраические объекты, как квадратные многочлены, топологически. Я расскажу про работу Л. Бартольди и В. Некрашевича, описывающую результат скручивания ушей у кролика Дуади.

Organization Committee e-mail:
dubna@mccme.ru