

Александр Игоревич Буфетов,
Михаил Константинович Миронов
Ортогональные полиномы и непересекающиеся пути
А. И. Буфетов и М. К. Миронов планируют провести 4 занятия.
Доступны 5 видеозаписей курса.
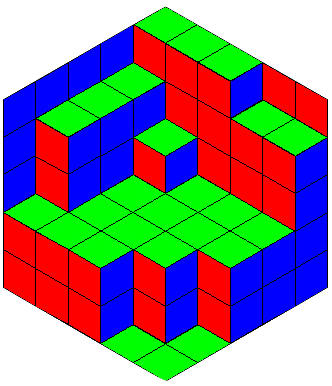
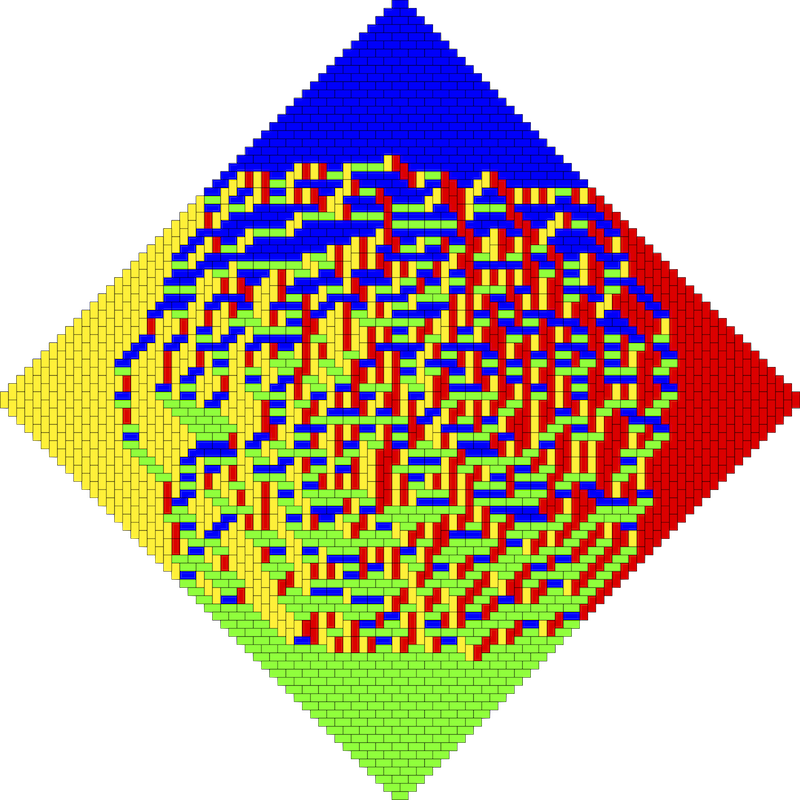
Непересекающиеся случайные пути возникают в самых разных комбинаторных задачах, например, в задаче о замощении шестиугольника ромбиками и в задаче о замощении ацтекского бриллианта доминошками.
При исследовании этих задач естественно возникают ортогональные полиномиальные ансамбли — распределения вероятностей, связанные с классическими семействами ортогональных полиномов дискретного переменного — например, ансамбль Хана в задаче о шестиугольнике и ансамбль Кравчука в задаче об ацтекском бриллианте.
В нашем курсе мы планируем подробно и элементарно разобрать несколько основных примеров. Впрочем, в ряде случаев развитие теории не пошло намного дальше разбора этих примеров. В этой области много замечательных открытых вопросов; некоторые мы сформулируем в курсе.
Для понимания курса вполне достаточно знакомства с самыми первыми понятиями линейной алгебры — скалярное произведение, матрица, детерминант матрицы. Знакомства с ортогональными полиномами не предполагается — мы подробно обсудим их на занятиях. Мы надеемся, тем самым, что наш курс доступен увлечённому школьнику.
Материалы
Картинки к этому анонсу взяты из брошюры Е. Ю. Смирнова «Три взгляда на ацтекский бриллиант», которую мы горячо рекомендуем нашим слушателям. Наш курс, однако, от нее независим.

Organization Committee e-mail:
dubna@mccme.ru
